Chi ha ucciso il Duca di Densmore?

Questo post è una traduzione e un adattamento di Qui a tué le duc de Densmore?, a propria volta un riassunto dell'omonimo racconto breve di Claude Berge.

Un giorno Sherlock Holmes ricevette una visita del proprio amico Watson, il quale era stato incaricato di indagare su un omicidio avvolto nel mistero da più di dieci anni.

All'epoca il Duca di Densmore fu ucciso da una bomba talmente potente da aver distrutto l'intero castello in cui viveva da quando andò in pensione. I giornali di allora riferirono che il suo testamento, anch'esso distrutto nell'esplosione, avrebbe dato grossi dispiaceri a una delle sette ex mogli. Poco prima di morire il Duca le aveva invitate tutte a passare qualche giorno nel proprio castello scozzese.

Holmes: Mi ricordo la faccenda. Quel che è strano è che la bomba fu congegnata precisamente per essere nascosta nell'armatura situata nella camera da letto, perciò suppongo che l'assassino debba per forza aver visitato più volte il castello.

Watson: Certo, perciò ho interrogato ciascuna delle ex mogli: Ann, Betty, Charlotte, Edith, Felicia, Georgia ed Helen. Mi hanno tutte giurato di essere state al castello una sola volta nelle loro vite.

Holmes: Uhm. E avete chiesto loro le date dei rispettivi soggiorni?

Watson: Suvvia Holmes! nessuno si ricorderebbe le date esatte dopo più di dieci anni. Ciononostante ho chiesto loro chi avessero incontrato al castello, e queste sono state le loro risposte:

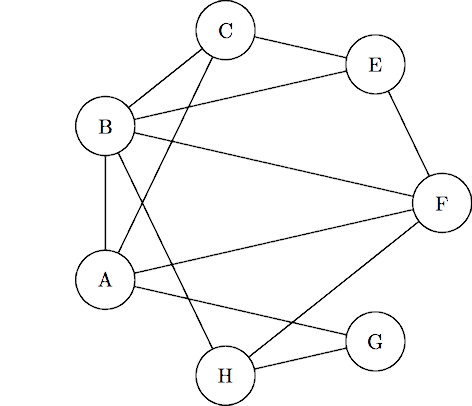
Ann ha incontrato Betty, Charlotte, Felicia e Georgia.
Betty ha incontrato Ann, Charlotte, Edith, Felicia ed Helen.
Charlotte ha incontrato Ann, Betty, e Edith.
Edith ha incontrato Betty, Charlotte e Felicia.
Felicia ha incontrato Ann, Betty, Edith ed Helen.
Georgia ha incontrato Ann ed Helen.
Helen ha incontrato Betty, Felicia e Georgia.

Watson: Come vedete, caro Holmes, le loro risposte combaciano!

Fu allora che Holmes prese una matita e disegnò questa strana figura:

Poi, dopo neanche trenta secondi, esclamò:

Holmes: Guarda, guarda! Quello che mi hai detto è sufficiente per determinare chi sia stata l'assassina!

Ma chi è dunque l'assassina, e quante volte al minimo è stata nel castello?